采用DSA形稳电极电化学催化降解废水的影响因素很多,并且各因素之间存在交互作用。响应曲面法(responsesurfacemethodology,RSM)是数学和统计方法结合的产物,通过合理的实验设计,获取实验数据,并基于该数据构建各影响因素和响应之间的多元回归方程,进而确定最佳的优化参数。RSM所需要的实验组数较少,可节省人力物力,多元回归方程容易建立,并且能够评价各因素间的交互作用,因而得到广泛应用。虽然有研究将RSM应用于化学和电催化工艺条件的优化,将RSM应用于优化DSA形稳电极电化学直接氧化处理废水的报道尚未见到。鉴于此,本研究以钛片为基底,采用涂层热分解法制备Ti/SnO2-Sb电极,并选用亚甲基蓝溶液作为模拟染料废水,以初始pH、施加电压和阴阳极距离为影响因素,电化学降解过程中的脱色率作为响应值,基于中心复合实验设计进行响应曲面分析,研究各个因素及其交互作用对于脱色率响应值的影响,进而确定电解脱色性能最优时的最佳电化学工艺参数水平值。
一、实验材料和方法
1.1 Ti/SnO2-Sb电极制备
按照实验需求裁剪钛片,钛片表面洗涤除油后,放入超声波清洗器中,分别用无水酒精和蒸馏水各清洗10min。将清洗好的钛片放入10%(质量)草酸溶液中水浴刻蚀180min[18-19],温度保持在100℃,当刻蚀后的钛片表面呈麻灰色面,取出钛片并用蒸馏水冲洗干净,晾干备用。称取1.25g的SbCl3和30g的SnCl4•5H2O溶解于50ml正丁醇中,再加入2.5ml浓HCl与0.05%(质量)十二烷基磺酸钠,混合均匀搅拌30min,活性层溶液盛放于瓶中备用。将刻蚀后的钛片放在活性层溶液中浸涂3min,取出后置于红外快速干燥箱中烘干5min,重复以上操作30次。其中每隔5次取出放入高温干燥炉中煅烧30min,温度为450℃,最后一次煅烧时长为1h,温度为550℃。
1.2 Ti/SnO2-Sb电极的表征
环境扫描电镜(FE-SEM)采用日本Hitachi的S4800,加速电压为5.0kV。X射线衍射仪(XRD)测试采用日本理学公司SmartLabX射线衍射仪,使用Cu/Kα辐射(λ=1.5424Å(1Å=0.1nm)),扫描范围20°~80°,扫描速率为0.2s/step,扫描步长为0.02°。
1.3 电化学水处理及溶液脱色率计算
配制亚甲基蓝溶液为模拟染料废水,电解实验采用可调稳压直流电源,将装好电解液的自制反应池置于磁力搅拌器上,电化学水处理时电源正极连接Ti/SnO2-Sb电极,负极连接Ni电极。使用紫外可见分光光度计对亚甲基蓝溶液进行扫描,获得最大吸收波长处的吸光度值,通过式(1)计算亚甲基蓝的脱色率
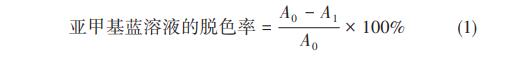
式中,A0表示电解前的亚甲基蓝溶液吸光度,A1表示经电解后亚甲基蓝溶液在最大吸收波长处吸光度。
1.4 响应曲面法实验设计
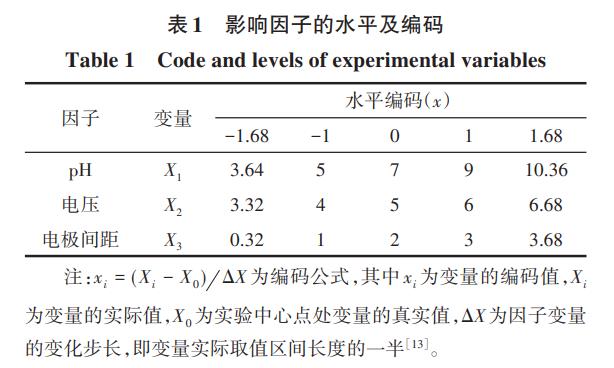
实验采用三因素二水平的五阶全因子中心复合设计(CCD),并用二阶RSM进行回归拟合实验,优化电催化氧化反应参数。选择初始pH(X1),电压值(X2)和电极间距(X3)为影响染料脱色率的三个参数因子,根据中心复合设计原理,先对脱色率做单因素实验,当pH为7,电压为5.0V,电极间距3cm时脱色率最大。由此给出各因子变量的合理变化范围:pH为3.64~10.36,电压为3.32~6.68V,电极间距为0.32~3.68cm。设计中的每个参数均在五个不同的水平(-1.68,-1,0,1,1.68)下进行研究。所有变量都围绕数值为0的中心点进行设计,实验中的每个变量都要在至少两个水平上进行实验,进而寻找最优点附近的响应面区域。分析实验数据的二次多项式模型如式(2)所示
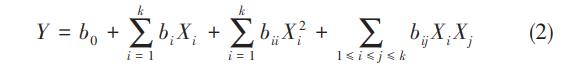
式中,Y为脱色率的响应曲面值;b0为常系数;bi是线性效应的回归系数;bii为二次效应的回归系数;bij为交互作用的回归系数;Xi为实验变量编码。统计软件STATISTICA用于将实验数据拟合为二阶多项式方程。确定系数R2评估实验因素的交互作用对观察响应值的影响程度,其值始终在0和1之间。R2值越接近1,说明模型预测响应越好。表1给出各因子水平的实际取值及其编码。
二、实验结果与讨论
2.1 Ti/SnO2-Sb电极表征
2.1.1 Ti/SnO2-Sb电极的扫描电镜
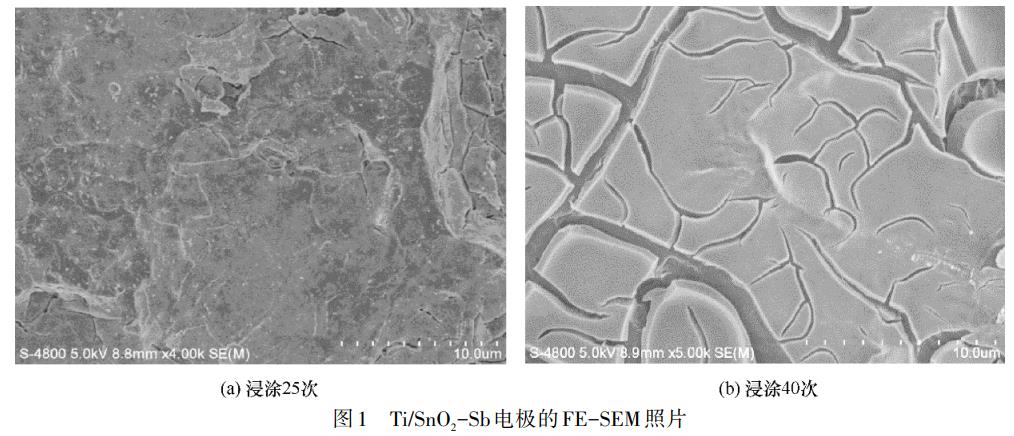
图1(a)是Ti/SnO2-Sb浸涂25次电极的FE-SEM图片,由扫描电镜图片可以看出电极表面整体平整。涂刷次数增大,可以增大电催化活性材料的负载量,缺点在于高温煅烧,电极的表面出现龟裂[图1(b),浸涂40次],降低了电极致密度,会导致电极表面钝化。实际操作中,电极刷涂次数控制在20~30次。
2.1.2 Ti/SnO2-Sb电极的伏安曲线
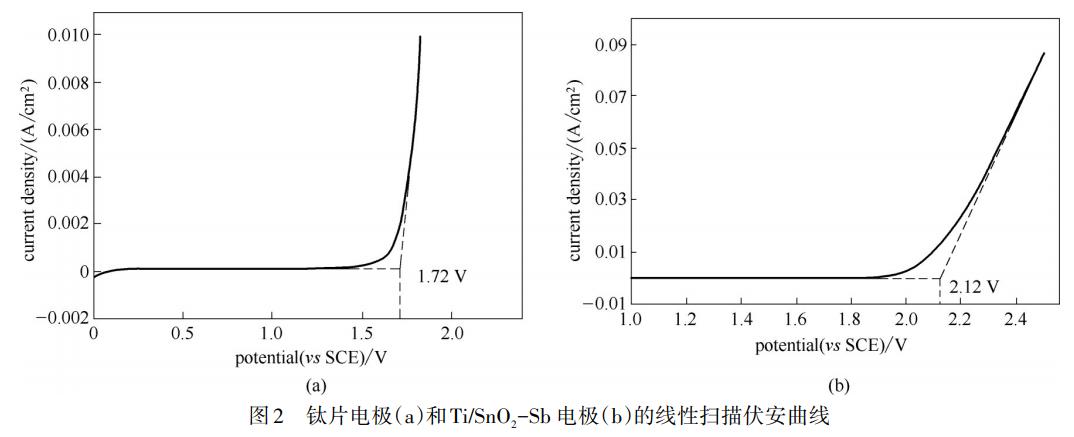
图2是钛电极和Ti/SnO2-Sb电极的线性扫描伏安特性曲线,曲线前段平滑,后段较为陡峭,前后段延长线的交点对应值是电极的析氧电位。Ti/SnO2-Sb电极的析氧电位为2.12V,纯钛板电极的析氧电位为1.72V,由此可见,涂覆电催化活性层后析氧电位大幅度增加。在电催化降解实验中,析氧电位越高,Ti/SnO2-Sb电极表面越难析出氧气,从而抑制电解水副反应的发生,有利于电催化分解污染物,提高电流的利用率和电解脱色效果。
2.1.3 Ti/SnO2-Sb电极的X射线衍射分析
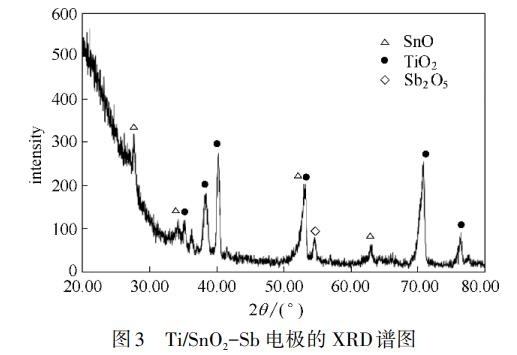
图3主要为TiO2衍射峰,2θ在35.3°、38.3°、40.2°、53.2°、70.9°、76.4°的衍射峰分别对应TiO2的(100)、(002)、(101)、(102)、(103)、(112)晶面[23];2θ在26.2°、34.1°、52.8°、62.9°的衍射峰分别对应SnO2的(110)、(101)、(211)、(310)晶面,SnO2以四方金红石结构存在[24]。2θ在54.6°的衍射峰对应Sb2O5的(620)晶面。此时三种金属氧化物之间的晶格十分相似,都以金红石型晶型存在,三种氧化物之间能够形成稳定结构,保持良好的电催化性能。
2.2 基于中心复合设计的响应曲面法优化实验条件
2.2.1 中心复合实验设计(CCD)及结果
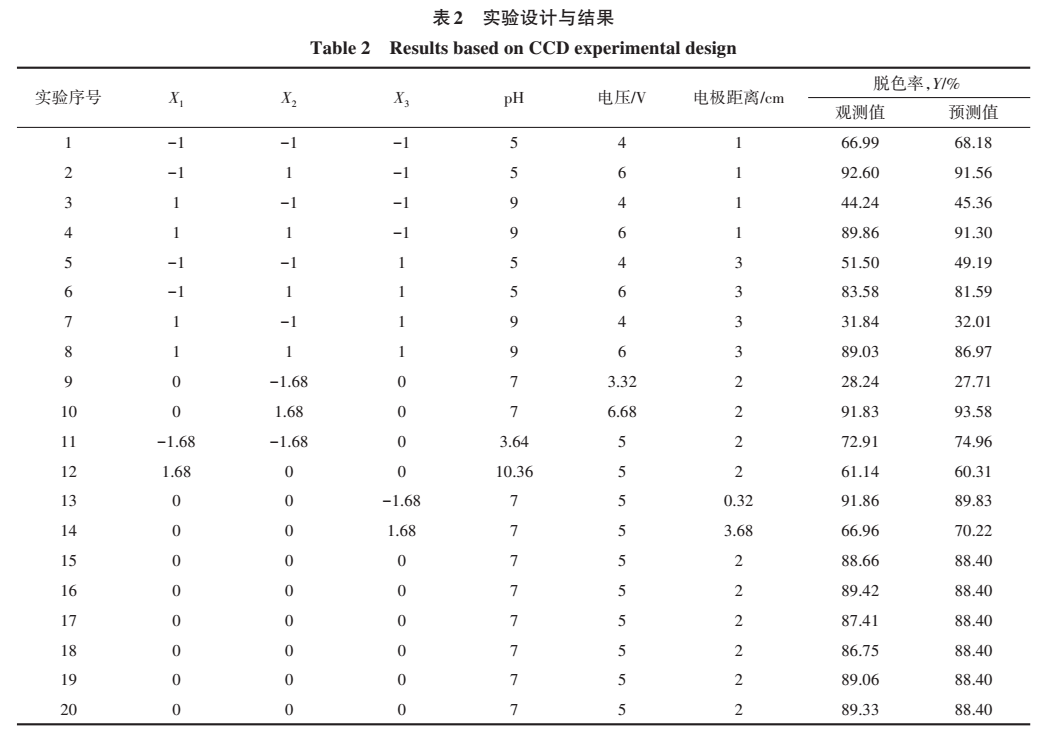
响应曲面法可以通过分析实验数据优化实验条件,有效快速寻找最佳实验方案。本研究共进行了20组参比实验,并且20组实验均无固定顺序,以降低外部条件对实验结果的干扰。利用基于中心复合实验设计的响应曲面法进行实验设计,实验设计和结果如表2所示。
2.2.2 模型拟合和精确性分析
根据表2的实验设计与结果,采用统计软件STATISTICA对数据进行分析,可将实验数据拟合为二次多项回归方程
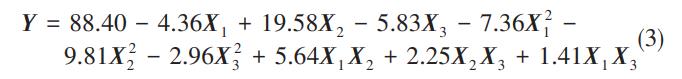
式中,Y为脱色效率的响应值,X1为初始pH,X2为施加电压值,X3为电极间距。
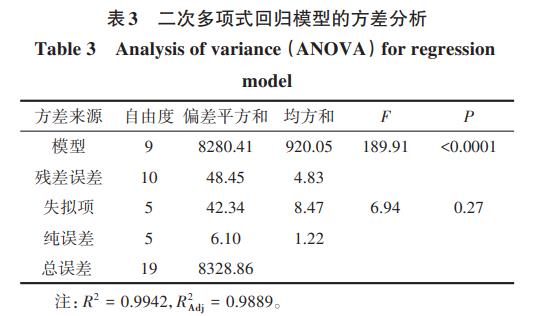
表3给出回归模型的方差分析结果,实验选用模型的F值为189.91,且P0.05,说明模型是合适的;模型的校正决定系数R2Adj=0.9889,说明该模型能解释98.89%响应值的变化,仅有大概1.11%的总变异不能用该模型解释;模型的相关系数为R2=0.9942,几乎接近于1,说明该模型拟合度良好,实验误差小,可以用该模型来解释和分析染料的脱色率。
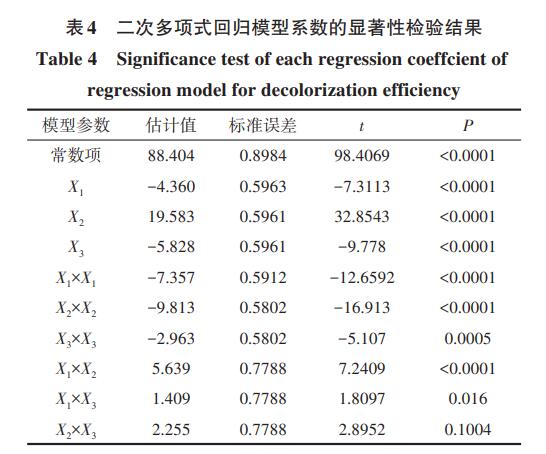
由表4不难看出,初始pH(X1)、施加电压值(X2)、电极间距(X3)对染料颜色去除率(即脱色率)都有显著影响。在模型分析中P≤0.05,说明所选模型的可信度高。表4给出CCD实验数据的回归结果可以观察到电压和电极间距的交互作用(X2×X3)对应的P=0.1004>0.05,所以电压和电极间距的相互作用对脱色效率的影响不太显著。其他变量的P值均小于0.05,说明这些变量对染料颜色去除率的响应值有显著的影响。因此脱色率的最佳回归模型方程可用式(4)表示
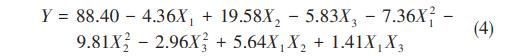
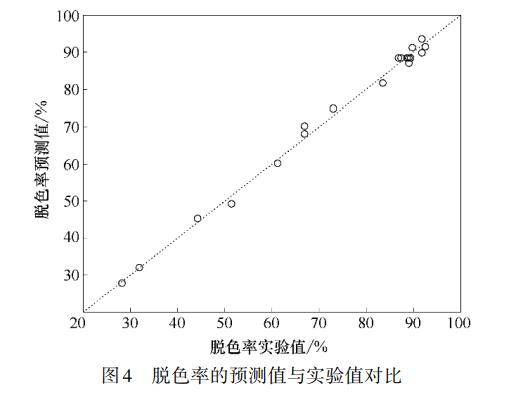
图4表明了脱色率的预测值与实验值的关系,可以看出预测值基本落在实验数据点周围,它们基本分布在直线y=x上,说明该模型的预测性能良好,进一步说明了该模型的有效性。以上分析表明该模型可以较准确地说明各个变量和脱色率之间的关系,同时可以对亚甲基蓝脱色的最佳条件进行较为精准的预测。
2.3 响应曲面法数据分析
响应曲面等高线图的形状可以直观反映各因素变量对响应值的影响,若形状为圆形,则表示各因素变量的交互作用不显著;若为椭圆形,则表示交互作用显著,从而可根据等高线图找出最佳的因素设置水平以及各因素之间的相互作用。3D图反映了响应曲面函数的形状,其轮廓呈凸起、凹陷或者马鞍形状则说明两个变量之间的交互作用显著,即两个变量因素的交互效应强。三个变量因素的响应曲面及其等高线图如图5所示。响应曲面图表明亚甲基蓝染料的脱色效率不仅依赖于施加电压值,pH和电极间距对其脱色效率的影响也不可忽略。所以基于各变量之间的响应曲面图,分析各变量对染料脱色效率的具体影响,寻找采用Ti/SnO2-Sb电极电化学处理亚甲基蓝染料的最佳脱色条件。
2.3.1 响应曲面分析初始pH的影响
通过调节染料溶液的pH(3.64,5,7,9,10.36)来研究其对电化学脱色实验的影响。从图5可以清楚地看到pH对脱色率的影响显著,最佳pH在6~7.5之间。当pH为酸性与碱性情况下,脱色效率较低,当pH在中性条件附近,脱色效率明显提高。这说明合适的pH有利于Ti/SnO2-Sb电极电催化氧化降解染料中的亚甲基蓝。从表2中可以看出在电压为5.0V和间距2cm情况下,pH为3.64、7、10.36时各自对应脱色率的预测值为74.96%、88.40%、60.31%,进一步说明了中性pH条件下有利于亚甲基蓝的电催化降解,实际实验中调节溶液的pH为中性非常有必要。
2.3.2 响应曲面分析施加电压的影响
测试了3.32、4、5、6、6.68V五组不同电压对电化学催化反应的影响,不论在实验过程中,还是最终的数据分析,都能观察到电压升高对电化学降解有促进作用。从表2可以看出在其他条件相同时,电压为6.68V时最高脱色率达到93.58%,但并不是电压越高越好,高电压情况下能耗随之增加,在电解实验过程中发现,在高电压下,阳极会产生更多副产物,有黑色泡沫状物质浮于电解液上方。通过图5可清楚看出随着电压的变化,电压和pH、电极间距的相互作用明显改变,存在着最优响应曲面,即电压处于6.0V附近,使得这种相互作用更为有效。

2.3.3 响应曲面分析电极间距的影响
如表2所示,电极间距对脱色率的影响不可忽略。其他条件相同,电极间距越小,脱色效果越好。如在pH=9,电压=6.0V情况下,电极间距为3cm时的脱色效率为86.97%,电极间距为1cm时的脱色效率为91.30%,在电极间距相差2cm情况下,脱色率相差4.33%,说明电极间距对电化学降解染料效果存在影响,但影响程度不大。缩短电极间距有利于电催化分解污染物,但电极间距过小时,溶液在电极间的流速变慢,使得传质效果削弱不利于电解反应,这个解释可以从第13组实验和第15组实验的观察值和预测值中得以验证。根据图5估算最佳电极间距在0.5~1.5cm之间。
2.4 响应曲面法分析亚甲基蓝脱色最佳实验条件及实验验证
应用响应曲面法对最佳实验条件进行预测,通过统计软件STATISTICA给出的结果可验证以上分析,从而可得实验的最佳条件:pH=6.98,电压=6.0V,电极间距=1.01cm,并且在最佳条件下,脱色率的预测值为98.68%。为了验证响应曲面法的计算结果在实际操作中具有良好预测效果,在最佳实验条件下进行三组平行验证实验,电解30min后立即将电解液利用紫外-可见分光光度计检测吸光度,并计算脱色率。三组验证实验的亚甲基蓝染料溶液脱色率分别为:97.85%、98.54%、99.03%,平均值等于98.47%,非常接近预测值。电解30min后,COD去除率才能达到78.6%,COD的去除率要明显滞后和低于脱色率。研究结果表明运用响应曲面法对染料脱色最佳条件的预测具有高的精准性和可信度。
三、结论
本文采用中心复合设计的响应曲面法预测和优化亚甲基蓝染料废水电化学脱色的最佳实验条件。实验中使用Ti/SnO2-Sb电极作为阳极,应用基于CCD的RSM模型对实验最佳条件进行预测,不需要大量的实验,节省实验次数和资源消耗,并提供有效工艺参数优化信息,此外,CCD有利于找到最佳实验条件。研究表明可以使用响应曲面法对亚甲基蓝染料电解脱色最佳实验条件进行预测,预测准确性高,相关系数R2=0.9942,模型精准有效。采用Ti/SnO2-Sb电极电化学脱色亚甲基蓝效果显著,实验的最佳条件:pH=6.98,电压=6.0V,电极间距=1.01cm,最佳条件下脱色率预测值为98.68%。实际处理废水时三次脱色率平均值98.47%,模型优化的预测值和实际电解的实测值吻合。该方法可用于优化电催化降解染料废水的工艺参数,为实际染料废水处理提供最优解决方案,可有效避免实验的盲目性。
如需要产品及技术服务,请拨打服务热线:13659219533
选择陕西博泰达水处理科技有限公司,你永远值得信赖的产品!
了解更多,请点击www.botaida.com