随着经济的快速发展,城市和工业污泥的产量日益增多,污泥的处置问题受到越来越多的重视。污泥是污水处理的终端产物,未经处理的污泥含水率高、体积庞大、成分复杂,处置不当易造成二次污泥。在众多处置方法中,流化床焚烧技术因其燃烧充分、处理速度快、污染物排放低等显著优点在污泥处理行业得到了广泛的应用。湿污泥直接燃烧会导致热损失的增加,因此污泥干化是污泥处置过程中重要的步骤。流化床干化具有脱水率高、污染小、操作简单等优点,是污泥深度脱水的有效方式。在污泥流化床干化技术中,临界流化速度μmf是其重要的参数之一,对流化床的设计和运行有着指导作用。
在预测物料的μmf方面,国内外学者做了大量的研究,得到了许多μmf的经验公式。但由于物料性质和试验条件的不同,得出的经验公式有很大差异,至今还没有统一的μmf计算公式。在污泥流化研究中发现,含水率是影响μmf的重要因素之一。而前人有关μmf的试验,研究对象多为玻璃球、石英砂、煤样等,影响因素多为床温、粒径、压力等。有关污泥含水率对μmf影响的研究较少。为此,本文研究了不同含水率下污泥的流化特性,介绍了μmf经验公式的推导过程,其他种类污泥可以参考本文方法,通过简单的试验快速得到μmf的计算公式。
一、试验装置及步骤
1.1 试验工况及样品
临界流化速度μmf是流化态操作的最低速度。本文认为,床料的物性(密度、粒径分布、表面粘性等)和流化气体的物性(密度、动力粘度等)直接影响μmf,温度、压力等外因通过影响床料和气体的物性间接影响μmf。实际工程中流化床干燥设备的运行压力为常压,运行温度在100℃以下。由于试验中测得温度在100℃以下时,污泥颗粒的密度、粘性等随温度变化较小,且Saxena对白云石(20~500℃)的研究也表明温度对μmf影响较小,故选定试验温度为30℃,试验压力为0.1MPa。
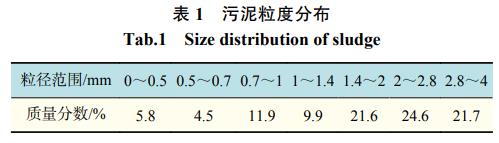
试验样品为东莞某造纸厂的造纸污泥,主要组成有纤维素、造纸填料、化工助剂和水。造纸污泥已经过机械压滤和破碎处理,初始含水率为48%,密度为1269kg/m3,呈颗粒状。污泥粒度分布列于表1,按质量百分比法计算污泥颗粒的质量平均直径dp为1.96mm:
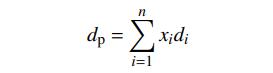
式中:di为颗粒直径,xi为质量百分比。
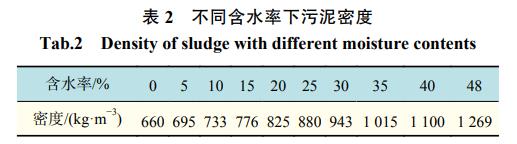
将收到的初始污泥颗粒置于105℃的烘箱内干燥8h,得到全干污泥,通过前后的质量差计算得到初始污泥的含水率为48%。在制备不同含水率的污泥时,首先取一个空托盘称重,再将适量含水率为48%的初始污泥置于托盘中,称量其总质量,计算烘干到目标含水率时这份污泥应该达到的目标质量。将污泥放入60℃的烘箱内干燥,每10min取出称重并混合均匀,直至达到目标质量,取出密封保存。使用同样的方法分别得到不同含水率的污泥样品,不同含水率下污泥密度参数列于表2。烘箱干燥的过程中会有部分颗粒破碎,为了防止粒度分布发生改变对试验结果造成影响,将干燥后的污泥筛分,按原粒度分布重新混合后用于试验。
1.2 试验装置
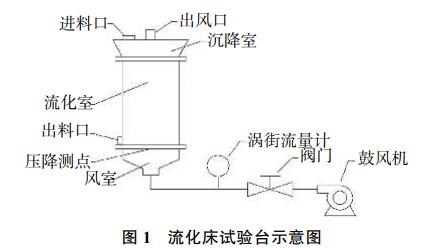
图1为试验装置简图。装置主要由流化床反应器、压差变送器、涡街流量计和离心式鼓风机组成。反应器的主体是一个直四棱柱流化室,其中一面设有有机玻璃,可观察流化室内流化情况,横截面积310mm×230mm,有效高度60cm。流化室底部设置有布风板、2层18目筛网和压板,布风板采用平板多孔式,错列布置,小孔风向与板垂直。反应器的上下部位分别是沉降室和风室,其截面呈上宽下窄的两个倒梯形。沉降室上宽下窄的结构使气体表观速度降低,有利于气流携带的细颗粒重新落回流化室内,减少细颗粒被气流带走而引起的压降变化,风室起导流和稳流的作用,使气流进入流化室时分布均匀。压差变送器一端布置于风室内接近布风板处,一端连接大气。离心式鼓风机配有高性能矢量变频器,通过控制鼓风机转速来控制引入风室的一次风量,通过LUGB–65涡街流量计测量空气体积流量,然后计算得到流化室内表观气体流速。
1.3 试验步骤
首先,测定空床状态下的布风板阻力,在空床状态下,调节变频器逐渐增大一次风量,在每个风量下维持2min,待系统稳定后,记录相应的布风板压降,直到增至最大风量。其次,称取10kg污泥颗粒床料,均匀加入至流化室内,关闭进料口,检查反应器的气密性是否良好。再次,开启变频器,启动风机,将风量调至最大,透过有机玻璃观察流化室内物料的流化状态,确认床内物料已完全流化,维持5min等待系统稳定。然后,调节变频器逐渐减小一次风量,在每个风量下,维持2min待系统稳定后,记录相应的压差变送器和涡街流量计读数,直至风量为零(变频器可调最大频率为50Hz,每次以2Hz逐步递减进行调节,共25组数据)。最后,待流化结束、床层高度较流化前略有增大时,记录此刻的床层高度,以用于计算料层空隙率。打开出料口,清空物料,换不同含水率的污泥重复以上步骤。
二、试验结果及分析
2.1 布风板阻力特性
试验已经测得了不同的一次风量下布风板的压降。风速u的计算如下:

式中:Qg为一次风量,Ac为床层截面积(经计算为0.0713m2),
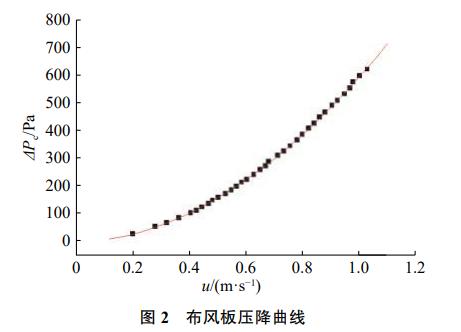
图2为布风板压降曲线,拟合得到布风板压降△Pc与表观风速u的函数关系为
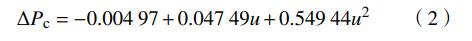
2.2 临界流化速度的确定
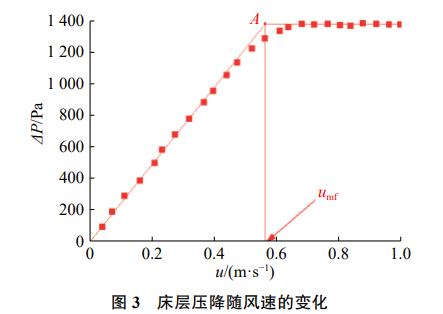
由固定床阶段进入流化阶段时需克服颗粒之间的作用力,升速法所得压降曲线由于体系的迟滞效应而带有任意性,因此颗粒的最小流化速度通常用降速法测定。本试验采用降速法,即先增大一次风量至床层完全流化,再逐次减小风量,并记录相应数据。试验可以测得污泥颗粒在不同表观风速u下,床层与布风板的压降之和,减去对应风速下空床布风板压降△Pc,即可得到床层压降△P随表观风速u的变化规律。将固定床阶段压降曲线与流化阶段压降曲线的切线交点定为临界流化点。图3为污泥含水率为0%时的风速–压降曲线,图中点A为临界流化点,对应的表观风速为临界流化速度μmf。
2.3 含水率对污泥流化的影响
图4为污泥含水率分别为15%和35%时流化过程现场图。图5给出了9种不同含水率污泥流化的风速–压降曲线。

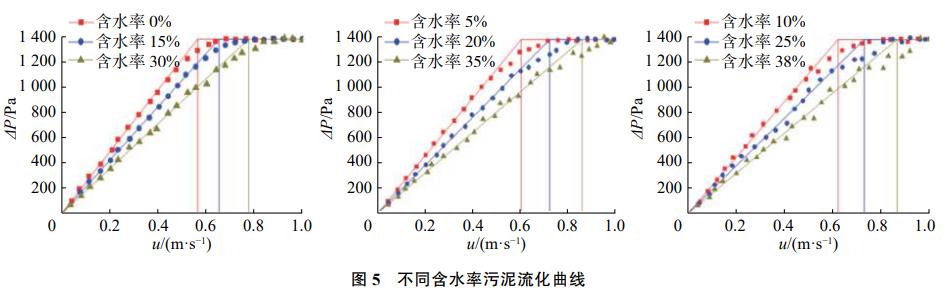
结合图4和图5,分析可知,随着污泥含水率的增大,μmf呈上升趋势,流化状态由散式流化向聚式流化过渡。一方面,含水率的增大使污泥颗粒的密度增大,而μmf与颗粒密度呈正相关,因此μmf随含水率的增大而增大。另一方面,在烘箱干燥过程中发现,试验所用造纸污泥含有许多絮状纤维,随着含水率的增大,污泥质地变软,且颗粒表面吸附了更多的水分,颗粒黏性和颗粒聚团能力明显增强。这使得污泥流化时颗粒与颗粒之间、颗粒与反应器壁面间的相互作用力均增大,流化阻力增大,从而使μmf增大。由图5还可知,含水率的增大使污泥流化稳定性降低。图5中不同含水率下的流化曲线表明:低含水率的污泥颗粒流化状态稳定,所得流化曲线平稳,在固定床阶段向流化阶段过渡时有平滑的拐点,试验观测流化室内呈散式流化,而高含水率的污泥颗粒流化状态逐渐恶化,所得流化曲线有较大波动,固定床阶段向流化阶段过渡的拐点不易确定,试验观测流化室内呈聚式流化。试验测得造纸污泥在此粒度分布下可流化的最大含水率约为38%,含水率高于38%时流化极不稳定,容易出现穿孔和沟流。
2.4 临界流化速度经验公式
国内外学者对μmf做了大量研究,得出很多μmf的经验公式,表3为部分学者得出的经验公式及公式适用条件。
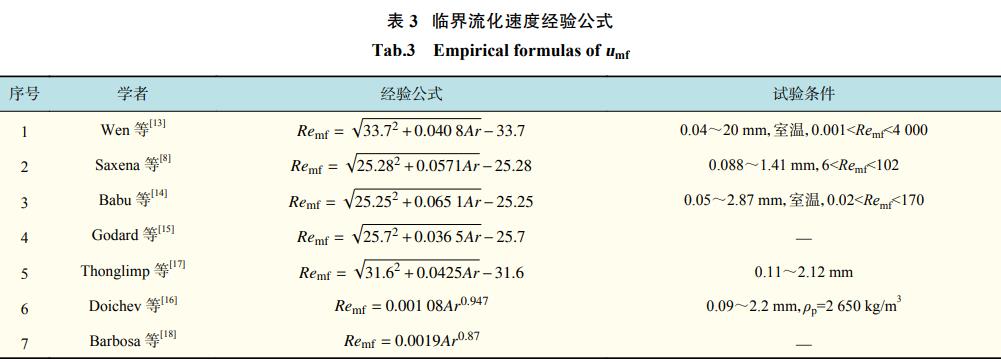
表3中,Ar为阿基米德数,Remf为临界流化时的雷诺数。
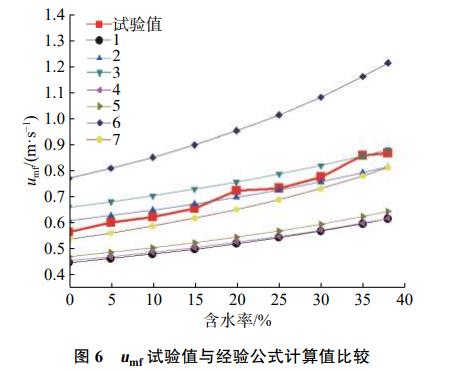
图6为本文μmf试验值与这些经验公式计算值的对比图,其中序号1~7分别对应于表3中的经验公式序号,红色粗实线为μmf随含水率的变化趋势。分析可知,由于物料流化性质的差异,直接使用这些经验公式来计算试验所用污泥的μmf会产生较大偏差,需选择合适的方法重新拟合经验公式。
计算μmf的经验公式虽多,但从公式的推导过程来分,基本可以分为以下两类。
2.4.1 第一类经验公式
此类公式以Wen等人的经验公式为代表,由床层压降与表观风速的厄贡方程推导而来。厄贡方程假设在临界流化状态时,床层压降近似等于气体对固体颗粒的拽力,忽略气体及床料与床壁间的摩擦力及内力。
在固定床阶段,床层压降与表观风速的关系式,可由厄贡方程准确表示为
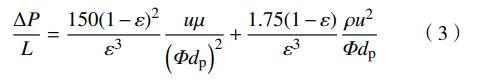
式中:L为床层高度,ε为料层空隙率,u为气体流速,即表观风速,Φ为颗粒球形度,ρ为气体密度,μ为气体动力黏度。
在临界流化状态时,床层压降等于单位面积上的料层重量,即
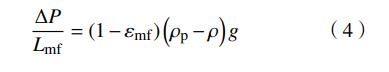
式中:ρp为物料颗粒密度,下标mf表示处于临界流化状态。
将式(3)和式(4)联立,并引入准则数
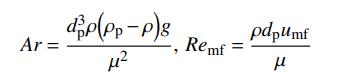
化简整理得到
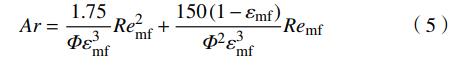
将式(5)看作Remf的一元二次方程,正根为
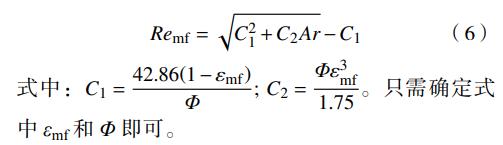
εmf和Φ的确定方法参考闫维平等所述:εmf为临界流化状态时的床层空隙率,略大于固定床时的空隙率。它实际上相当一个几乎没有重量的填充床的最疏松状态,可以由随意填充试验来测量。εmf取流化结束时的床层空隙率为
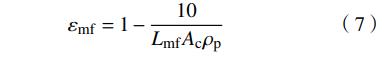
考虑到若εmf在各个含水率取不同值,Φ的值将很难确定,且测得不同含水率时的εmf变化很小,因此通过试验测得εmf算术平均值为0.414。将不同含水率下的污泥物性参数、μmf的试验值及εmf的算术平均值代入式(6),通过试凑法得到Φ的近似值。最后代入得到C1=16.09,C2=0.0445,进而得到μmf的经验公式。
由于低含水率的污泥颗粒比高含水率时流化稳定,试验偏差小,使用低含水率的几组数据拟合得到经验公式
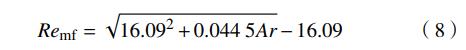
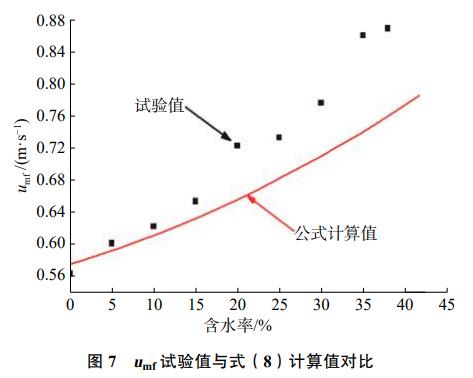
μmf试验值与式(8)计算值的对比如图7所示,显然,计算值与试验值偏差很大。分析原因是由于此类公式在应用厄贡方程时假设了床层压降等于气体对固体颗粒的拽力,而忽略了床料颗粒之间的内力。当试验样品为玻璃珠、石英砂等非黏性物料时计算较为准确。造纸污泥在低含水率时黏性较小,与上式偏差不大,但随着含水率的增大,污泥黏性增大,部分颗粒聚团,物料之间的内力足够大已不能忽略。因此试验值比计算值大,且含水率越高,偏差越大。
2.4.2 第二类经验公式
此类公式由单颗粒受力分析推导而来。
在临界流化现象发生时,单颗粒或颗粒团在床内主要受到3个力的作用,分别为颗粒本身的重力Fg、气体的浮力Ff、流化气体的拽力Fy,且这3个力相互平衡,即

该公式应用于多粒子系统时会有偏差,为了消除这种偏差,将式(10)整理成

此类公式最早由前苏联学者费多罗夫提出,此后学者们针对不同情况得到许多组a、b值,我国《层状燃烧及沸腾燃烧工业锅炉热力计算方法》中推荐的公式就属于此类。
基于试验数据,拟合得到经验公式
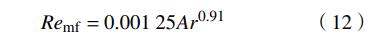
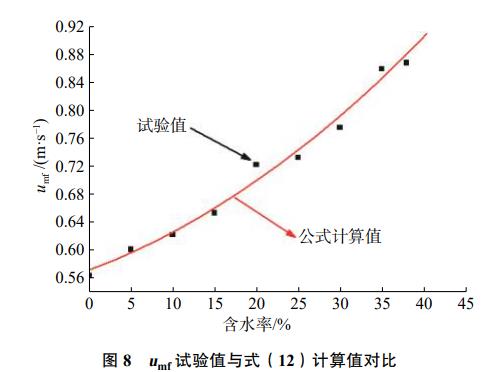
μmf试验值与式(12)计算值的对比如图8所示,可以看到计算值与试验值偏差较小,离散程度在5%以内,因此式(12)可用于此造纸污泥的μmf计算。
需要说明的是,由于城市及工业污泥种类繁多,流化性质差异很大,其他种类的污泥若直接套用式(12),可能造成一定偏差,甚至此造纸污泥在不同的粒度分布下,μmf也可能不同。虽然此式不具备广泛通用性,但其他种类的污泥可参考式(11),通过几组流化试验来确定a和b,即可得到可用的μmf计算公式。
三、结 论
本试验在常压0.1MPa和常温30℃下,以空气为流化气体,测量了含水率从0%~38%的造纸污泥临界流化速度μmf。此外,将试验结果与现有经验公式进行对比与分析后,选用合适的方法重新拟合了μmf的经验公式,得到如下结论:
a.造纸污泥在试验粒度分布下,低含水率时呈散式流化,随着含水率的增大,逐渐向聚式流化过渡,含水率高于38%时难以流化,此时极易发生穿孔和沟流。
b.污泥颗粒的μmf随含水率的增大而增大。
c.此造纸污泥的μmf,可以用公式Remf=0.00125Ar0.91来计算,误差在5%以内。
d.在主流的两类经验公式中,形如Remf=aArb的经验公式在计算污泥的μmf时误差较小。( >
如需要产品及技术服务,请拨打服务热线:13659219533
选择陕西博泰达水处理科技有限公司,你永远值得信赖的产品!
了解更多,请点击www.botaida.com